LAS MADERAS TAMBIÉN NOS HABLAN
Cuando queremos averiguar algo de nuestra historia, lo inmediato es recurrir a documentos escritos, si es que tenemos la fortuna de encontrarlos.
Pero no siempre se encuentran y en nuestra ayuda surgieron los arqueólogos que aprendieron a interpretar los restos que sobrevivieron a la destrucción del conjunto al que pertenecieron.
En nuestras tierras disponemos de una espectacular carpintería, de la que podemos estar muy orgullosos, y lógicamente nos gustaría saber como pudo surgir algo tan complejo, para lo cual es inmediato recurrir a la historia, que no siempre coincide con lo que nos cuentan sus maderas.
Llevo más de treinta años tratando de interpretar lo que las maderas me dicen,
O simplemente las investigo, cuando se presenta la ocasión de traspasar su vistoso intradós, pudiendo analizar su técnica constructiva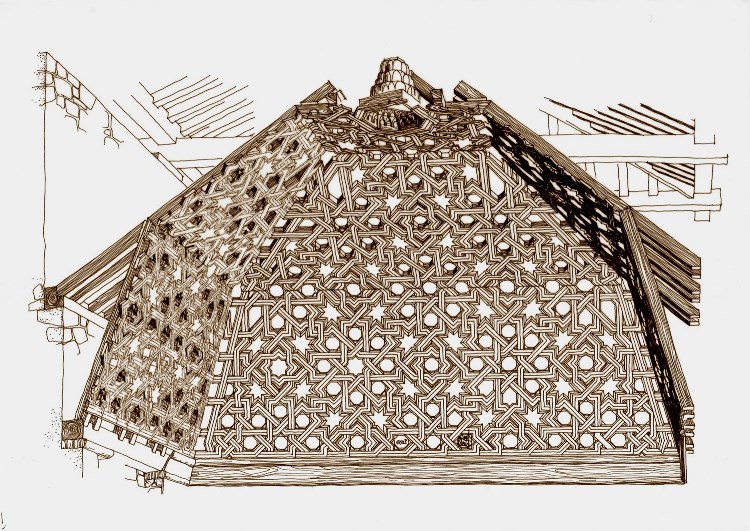
Para dejar a quienes vengan detrás la máxima información posible
Incluso en alguna ocasión viajando más de 700 km en un solo día, para poder analizar la parte oculta de un artesonado, prácticamente desconocido, cuyo interior pude fotografiar años atrás
Y así poder comprobar si el dibujo que entonces había realizado, basándome exclusivamente en la lógica constructiva, era correcto o debía corregirlo
O investigando como se podían realizar las armaduras más complejas, es decir la media naranja de lazo lefe, que figuraba en las ordenanzas para el examen del geométrico, máxima categoría de los carpinteros de lo blanco
Incluso construyendo uno de su doce gajos. Así algún día, cuando convoquen exámenes de geométrico, tal vez pueda presentarme y aprobarlo.
El principal problema con que nos encontramos para poder investigar sus orígenes, es la inexistencia de ejemplares de la alta edad media que hayan sobrevivido, así como la falta de documentos que nos hablen de los desaparecidos.
Gómez-Moreno, uno de nuestros más insignes historiadores del arte y de la arquitectura, opinaba que el origen de esa carpintería había que buscarlo entre los almohades, como posibles interpretes de la carpintería que los romanos usaron en sus construcciones. (Foto Gonzalo Menéndez-Pidal)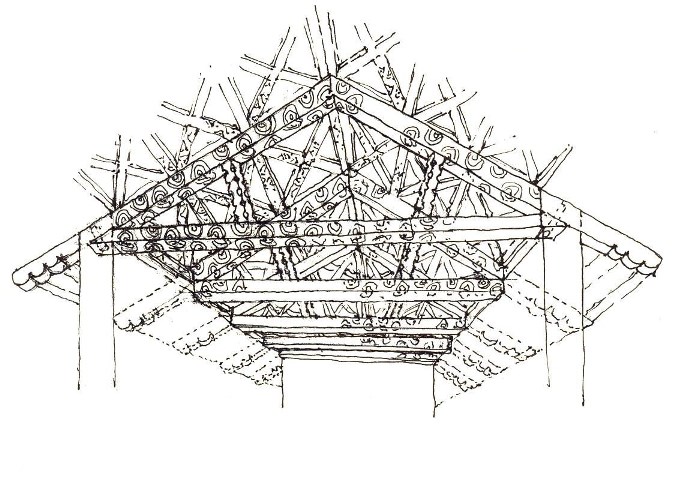
Don Manuel trató de relacionar alguna de nuestras armaduras más antiguas, como esta del Salvador de Priesca, con las romanas (Dibujo Rafael Manzano)
y tal vez las relaciona con las que se hicieron en Marruecos, como esta de la mezquita Qarqwiyin de Fez
Ahora bien, si por su apariencia, D. Manuel podía equiparar las armaduras de par y nudillo, con alguna romana, pongo por caso la de Santa María in Cosmedin, 
No tuvo en cuenta de que en su concepción, las romanas y las castellanas son soluciones radicalmente diferentes. La techumbre romana corta la longitud de la nave mediante cuchillos triangulados (sea cual sea la forma de la triangulación), sobre los que apoyan tramos concebidos como los forjados de piso, pero inclinados para dar salida a las aguas de lluvia, a diferencia de nuestras armaduras de pares
que, tengan o no nudillo, consisten en parejas de maderos cuyo equilibrio es similar al de los naipes que aquí muestro. 
Lógicamente, condicionado por la rugosidad de la superficie en la que se apoyasen, así como por la inclinación escogida, que cuanto menor sea, más difícil será conseguirlo.
Los mismos problemas plantean las armaduras castellanas, es importante contener los empujes de los pares en sus apoyos, y cuanto menos inclinados los coloquemos, menores serán sus empujes. 
La base de nuestra carpintería histórica coincide técnicamente con la más antigua conocida de los pueblos del norte de Europa, y tratándose de un sistema constructivo radicalmente distinto al romano, considero muy poco probable que nuestras armaduras históricas deriven de la carpintería de armar romana. Incluso, aunque los almohades fueron transmisores de lo realizado por Roma, difícilmente pudieron aprender lo que allí nunca se realizó.
Una posible explicación sería que tal vez nos aportaran alguna técnica proveniente del extenso mundo islámico.
Esta fue mi primera hipótesis de trabajo, y nada más sencillo que indagar en el amplio territorio islámico para buscar carpinterías similares, que hubieran podido ser sus precursoras. 
Pero por más que busqué y rebusqué sobre lo realizado en los amplios territorios en los que se desarrolló el Islam, todo lo que encontraba era similar a lo que aquí muestro
las armaduras de cubiertas a dos aguas tan sólo aparecían en sus territorios más septentrionales: Turquía o Siria, pero si excepcionalmente existen, al estudiarlas, vemos que responden a modelos de la tradición romana, 
Siempre que excepcionalmente encontraba alguna techumbre, como por ejemplo la de iglesia de Santa Catalina del Monte Sión, o la de la basílica que conmemora el nacimiento de Jesús, en Belén, el modelo utilizado era sistemáticamente el de cuchillos triangulados romanos.
Lo habitual en la mayoría de los territorios en los que se inició el Islam era construir las casas con terrazas planas o con cúpulas hemisféricas, pero nunca cubiertas inclinadas,
y si excepcionalmente entre los vastos conjuntos de terrazas planas encontramos alguna cubierta inclinada, suele ser en el África más occidental, realizada durante el periodo en el que esta zona dependió del Ándalus hispano, y siempre en algún edificio emblemático, en el que su promotor, precisamente había querido marcar la diferencia con el resto de lo allí realizado.

Para tratar de explicar qué pueden contarme las maderas que pasan por mis manos, pondré un ejemplo concreto, de algo que me ocurrió en Sevilla, hará poco más de veinte años, precisamente cuando me encontraba recuperando los artesonados del Palacio de Miguel de Mañara, a partir de sus menguados fragmentos
Caminaba por una calle del casco histórico, cuando me llamó la atención una pequeña pieza de madera junto al bordillo de la acera.
Sorprendentemente parecía una estrella
apenas pude creerlo, tenía todo el aspecto de ser un candilejo, tal vez de algún artesonado de lacería. Al tenerla en la mano ya no me cupo la menor duda, todos sus bordes superiores estaban biselados y sus cinco puntas confirmaban que efectivamente se trataba de un candilejo; naturalmente no dudé de echármela al bolsillo, dejando para la vuelta a Madrid la tarea de averiguar a que tipo de traza podría pertenecer aquella pieza y de donde podría haber salido.  El candilejo siempre el hueco dejado entre las cintas de un determinado trazado. Nada más simple que dibujar cintas rodeando totalmente al candilejo, y en la intersección de las dos que rodean su punta , trazo el eje de la calle correspondiente a la cinta horizontal
El candilejo siempre el hueco dejado entre las cintas de un determinado trazado. Nada más simple que dibujar cintas rodeando totalmente al candilejo, y en la intersección de las dos que rodean su punta , trazo el eje de la calle correspondiente a la cinta horizontal La otra cinta de la misma calle, será simétrica de la primera dibujada respecto al eje previamente trazado
La otra cinta de la misma calle, será simétrica de la primera dibujada respecto al eje previamente trazado
La otra cinta de la misma calle, será simétrica de la primera dibujada respecto al eje previamente trazado
Sigamos ahora haciendo lo mismo con otra de las cintas que bordea el candilejo
A partir de su eje, trazo la cinta paralela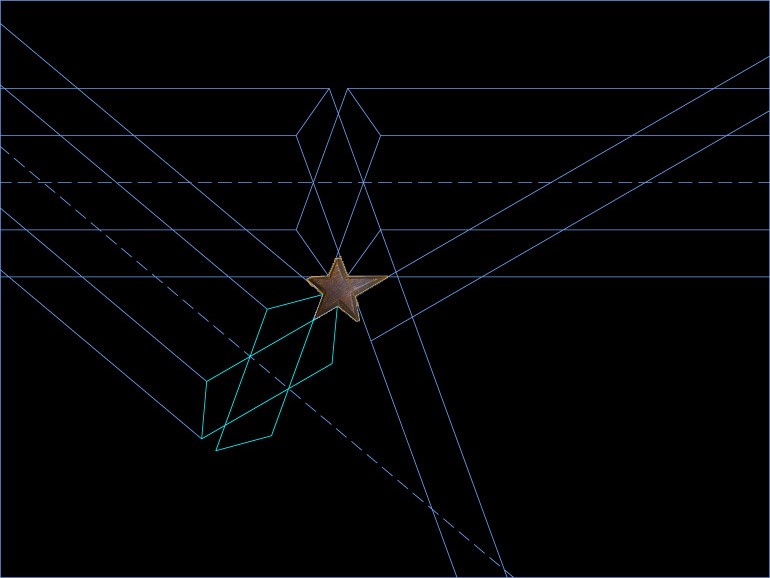
E inmediatamente, surge la aspilla correspondiente a esa calle.
Pero si me fijo en el candilejo y amplio el dibujo, podemos apreciar que su punta inferior derecha no sigue la alineación de la aspilla que acompaña a la punta superior. ¿Es un error?
No, esto es normal, ya que la rueda de la derecha ya no es de nueve, sino de doce y su aspilla no sigue las mismas reglas
Elimino por tanto dicha prolongación, y dibujo en verde y de trazos el eje de la calle correspondiente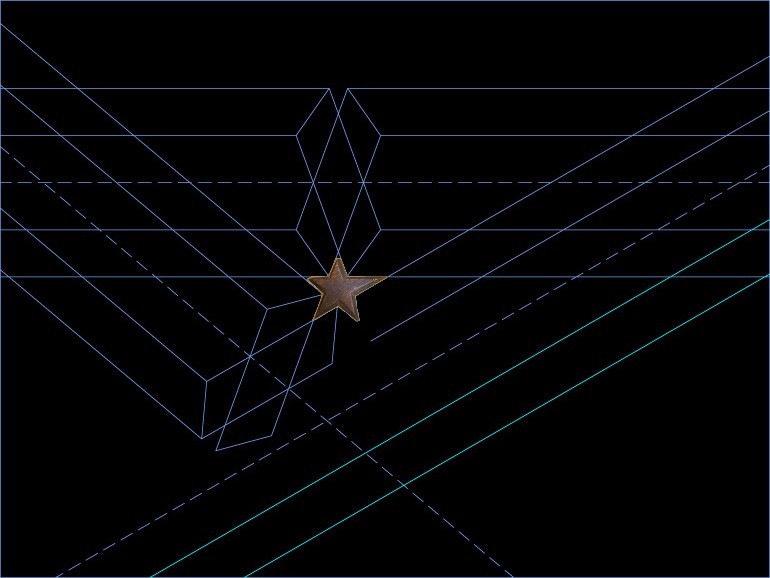
Como necesito la aspilla de la rueda de doce, dibujo de trazos y en verde el eje de simetría entre dos brazos adyacentes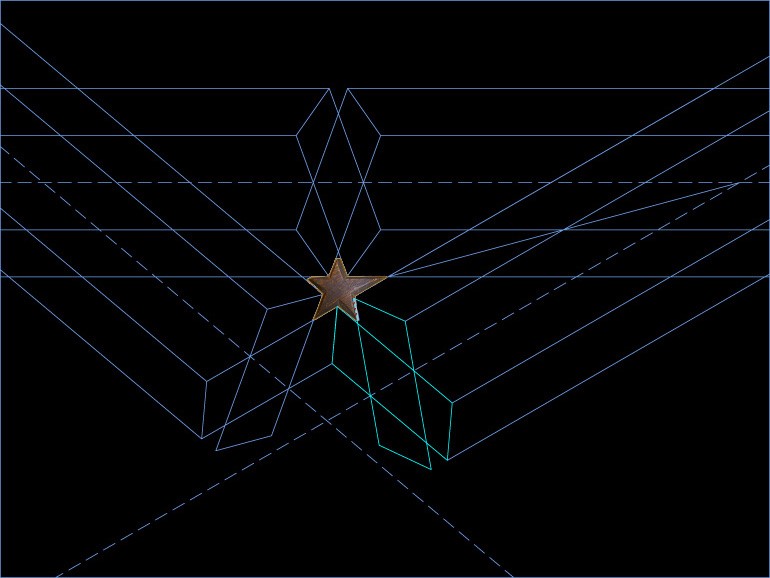
A partir del cual reproduzco la aspilla de la rueda de doce, que ahora si coincide con la punta del candilejo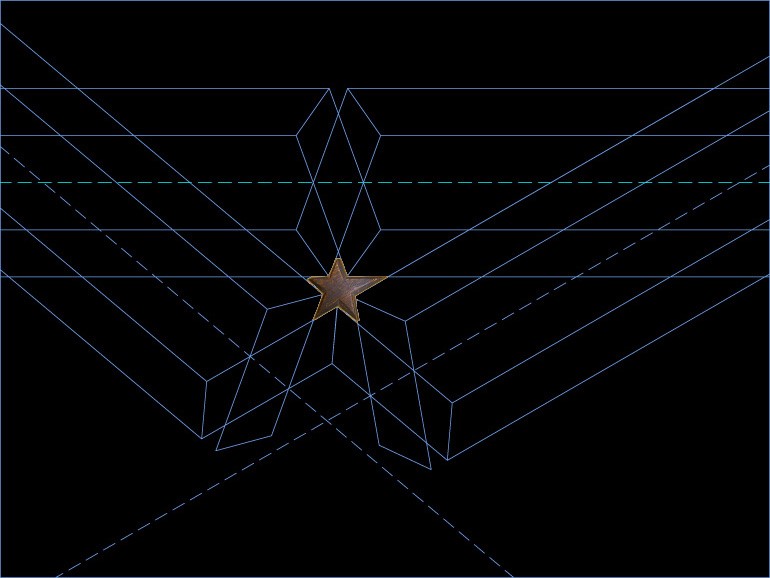
Si vuelvo al primer eje trazado
Puedo dibujar por simetría nuevos brazos de ambas ruedas
Y por semejante procedimiento podría seguir dibujando el resto de brazos de ambas ruedas
Ahora paso del esquema anterior en el que tan sólo me he preocupado de los bordes de las cintas a un dibujo con verdaderos taujeles, en el que las cintas se entrelazan, aspecto que los habituales gramiles – las ranuras que decoran la cara de los taujeles – acentuan al interrumpirse en los cruces
En definitiva, el candilejo nos dice que pertenece a un trazado en el que hay ruedas de nueve brazos y sus desculatadas de doce
Realmente el dibujo anterior tan sólo nos muestra una de las tres ruedas de doce que la de nueve puede desculatar
Tema que da origen a uno de los cuatro módulos básicos usados por los carpinteros castellanos de lazo.
Ese módulo es precisamente el triángulo equilátero cuyos vértices son los centros de las tres ruedas de doce brazos.
Una vez eliminado todo lo que sobra, sólo falta completar las aspillas que no desculataban ruedas
Lo que nos da este módulo triangular equilátero.
Pero no es lo único que la diminuta madera me podía contar, me queda averiguar de donde pudo venir.
En Madrid, con independencia de las deducciones anteriores, traté de recordar la calle en que encontré aquel candilejo, intentando visualizar lo que entonces hice, y llegué a la conclusión que fue tras salir del Palacio de Miguel de Mañara, sito en la calle Levíes, iba hacia la Plaza Nueva, y tras consultar un plano de Sevilla llegué a la conclusión de que fue precisamente en un tramo de la calle de San José, 
precisamente en la zona en que se encuentra la puerta de la iglesia del Convento de la Madre de Dios, por lo que mi primera impresión fue que tal vez allí habría una armadura con una composición de lazo de nueve y doce, 
y para comprobarlo, ni siquiera tuve que esperar al próximo viaje a Sevilla, entre mis libros enseguida encontré fotos del interior de la iglesia, y en su presbiterio cuatro espléndidas pechinas de lazo de nueve y doce, que daban apoyo a la espectacular ochava de cinco paños que culmina el artesonado, en este caso, una composición de ruedas de lazo de diez.
Y en alguno de aquellos triángulos, seguramente faltaría al menos un candilejo. 
A partir de las fotos compuse uno de los triángulos de aquella pechina, 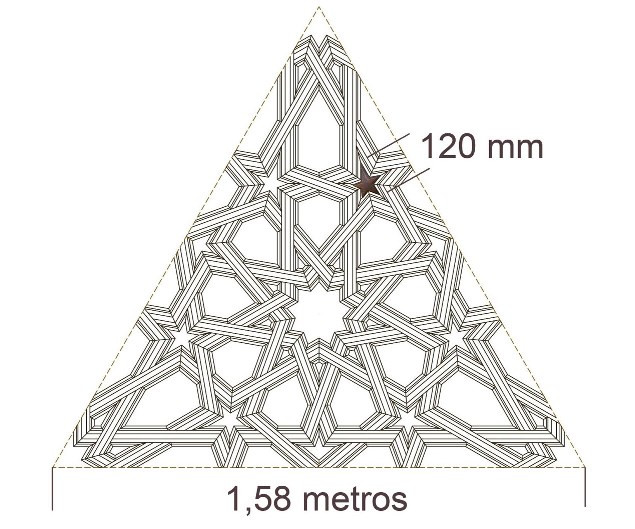
y a continuación, realicé un dibujo de su módulo básico teniendo en cuenta las medidas del candilejo, y aunque las que podía deducir de las fotos sólo fueran aproximadas, no me dejaron ninguna duda de que el candilejo se había desprendido de alguna de ellas. Tal vez barriendo la iglesia había acabado en la calle, y las patadas de algunos transeúntes lo habían llevado hasta el punto en que lo encontré.
Ningún documento justifica que este candilejo pertenezca a la mencionada iglesia, y ni siquiera he ido al lugar para medir la pechina original y confirmar mis deducciones, también podría haber buscado el lugar del que pudo haber caído y así encontrar el hueco que dejó y tratar de recolocarla en su sitio (por supuesto siempre que contara con una escalera adecuada), pero no hice nada de ello.
Es decir, no tengo ningún documento que me confirme que el candilejo es de aquella iglesia, ni he comprobado in situ que realmente es de allí, sin embargo, estoy absolutamente convencido de que lo es, por la simple razón de que el conjunto de deducciones realizadas me conducen inequívocamente a establecer esa conclusión.
En el ejemplo expuesto, se podría confirmar la veracidad de las deducciones realizadas, ¿pero que hacer cuando no disponemos de esa posibilidad? Podremos estar tan convencidos de nuestras conclusiones como en el caso del candilejo, pero tan sólo podrán tener categoría de hipótesis
Si queremos indagar en los orígenes de nuestra carpintería histórica, especialmente de la compleja de lacería, nos faltan documentos y restos suficientemente antiguos, y los más antiguos de que disponemos no nos aclaran mucho.
Y en ocasiones tenemos piezas de madera de armaduras originales, pero no es fácil manejarlas y analizarlas una a una.
Ahora me estoy refiriendo precisamente a un ejemplo segoviano: la iglesia de San Millán. Hace unos 20 años, a instancias de Antonio Ruiz Hernando, y acompañado de Miguel Fernández Cabo, a quien había dirigido su magnífica tesis sobre las techumbres leonesas, pude ver las maderas de su antigua techumbre, aunque no como ahora se encuentran, sino malamente amontonadas, de tal forma, que sólo se podían ver aisladas las que sobresalían del conjunto, y algunos detalles de las mismas, pero no los suficientes para poder establecer conclusiones indiscutibles.
Y aquellas maderas me decían que formaban parte de una armadura de par hilera, atirantada.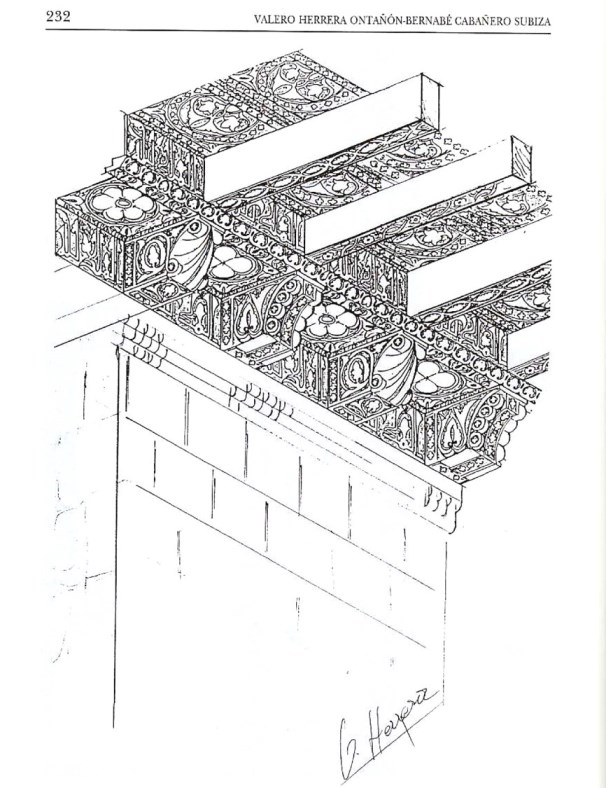
Un trabajo posterior de Valero Herrera Ontañón y Bernabé Cabañero Subiza, concluye que la nave de San Millán se cubría con una techumbre plana, al modo de la que en su día tuvo la Mezquita de Córdoba. Es un trabajo serio y muy bien documentado, cuyos argumentos no intento rebatir, pero en cambio, las maderas me están negando sus conclusiones.(Dibujo de Valero Herrera)
En ese texto se dice que la techumbre plana de San Millán era como la de la Mezquita de Córdoba, sin embargo, sus maderas de 11 x 19 cm distan mucho de parecerse a las cordobesas, de 30 x 30 cm. 
y si hacemos unos números, como los que constantemente tengo que hacer en obras y restauraciones, su frialdad niega que esas maderas de 11 x 19 cm se pudieran utilizar para formar un techo plano.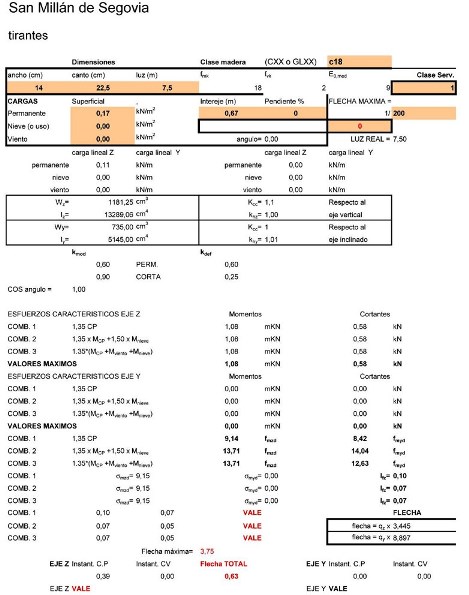
Tan sólo las vigas de mayor sección, sin carga alguna y consideradas como tirantes exclusivamente, cumplirían las condiciones mínimamente exigibles.
Por otra parte, la techumbre de Córdoba, a pesar de sus generosas secciones, y un clima menos agresivo que el segoviano, ya requirió en tiempo de Alfonso X una importante restauración.
¿Como pudo sobrevivir la techumbre de San Millán con un clima mucho menos favorable?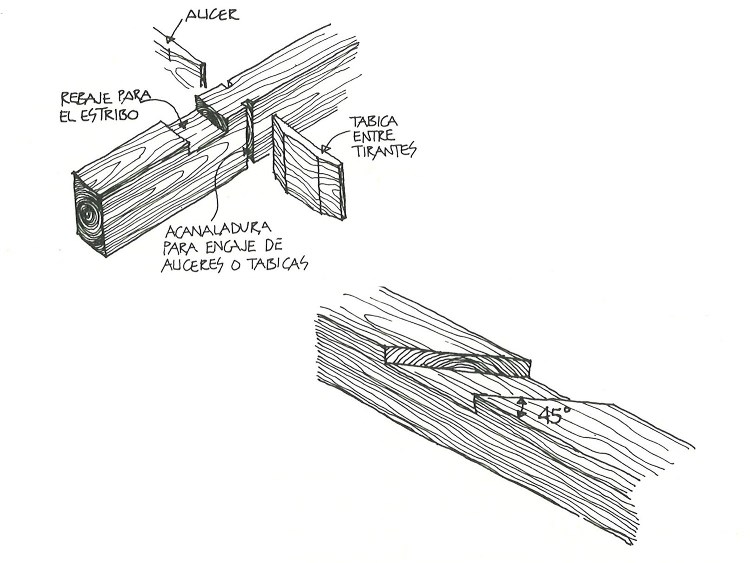
Por otra parte, aunque como ya he mencionado no pude ver todas las maderas allí apiladas, en alguna de las piezas de 14 x 24 cm, encontré rebajes típicos a los usados para encajar un estribo, con las correspondientes ranuras para sus aliceres o tabicas, y además, en una de ellas, Fernández Cabo apreció un rebaje a 45º, propio del encaje de un cuadral, Ambos detalles sugieren claramente su pertenencia a una armadura de pares, y no tienen ningún sentido en una techumbre plana.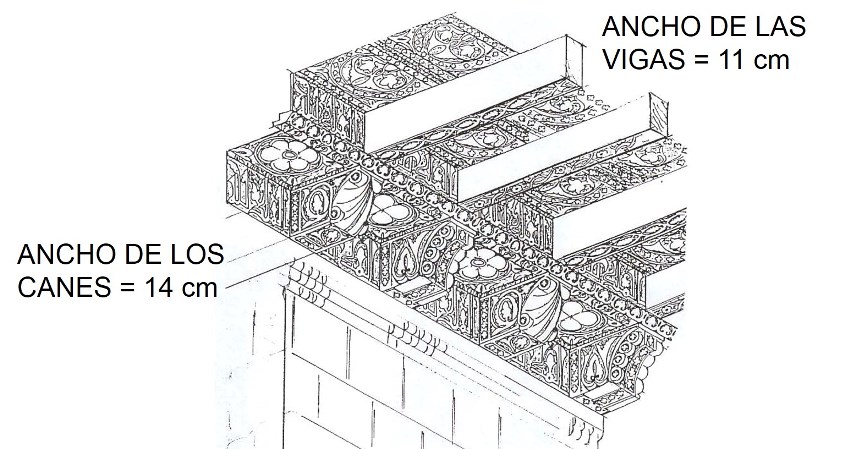
Por otra parte, según la hipótesis de techo plano, los canes tienen 14 cm de anchura y tan sólo 10,5 las vigas que en ellos apoyan. No digo que no sea posible, pero en más de treinta años hablando con las maderas, sería el primer caso en que esto ocurre, lo normal es que can y viga tengan la misma anchura.(Dibujo de Valero Herrera)
Es decir, se contraponen argumentos razonados y documentados a conclusiones tan sólo basadas en una fantástica conversación con sus maderas. Es evidente que por el momento, por mucho que el hecho me inquiete, que no puedo ofrecer más que pruebas circunstanciales que defiendan mi hipótesis, por lo que me tendré que resignar, como el abogado impotente que ve como condenan a su defendido a pesar de estar convencido de su inocencia.
Pero volvamos a la cuestión del origen de nuestra carpintería histórica.Cada vez estoy más firmemente convencido de que la técnica de organizar armaduras de cubiertas es de origen cristiano, anterior a la llegada del Islam a nuestros territorios, y que la incorporación de los temas geométricos a esta carpintería, aunque surgiera en la Granada Nazarí, sólo pudo ocurrir por haber heredado sus autores la técnica de origen celta o visigodo que se practicaba antes de la llegada del Islam a nuestra península
No creo que admita discusión el hecho de que una vez surgida esta espectacular carpintería, fue la dinastía Trastámara quien contribuyó de forma decisiva a que esa forma de organizar la cubierta de los edificios se extendiera, y después, ya consolidada, perdurara a lo largo de los siglos XVI y XVII, prolongándose lánguidamente incluso durante el XVIII.
Y precisamente Segovia fue uno de los lugares que miembros de esta dinastía escogieron para establecer su corte. Sabemos que en tiempo de Enrique III, su esposa, Catalina de Lancaster, encargó para el Alcázar el techo de la Sala de la Galera, 
y posteriormente, su nieto Enrique IV, realizaría el convento de San Antonio el Real, con sus magníficas techumbres. 
Desgraciadamente, en 1862 un incendio devastó el Alcázar, y se perdieron todas sus techumbres. Tan sólo se salvaron los chapiteles de dos torrecillas de vigilancia, al estar del lado del que arreciaba el viento. 
Aunque no tienen la categoría de las armaduras perdidas, no por ello dejan de ser piezas de gran interés, al estar entre los primeros chapiteles que, a instancias de Felipe II, se hicieron en Castilla al modo de los de Flandes, en este caso, con motivo de su boda con Ana de Austria.
Sin embrago, el Alcázar hoy vuelve a mostrarnos la silueta que tuvo antes de aquel pavoroso incendio. ¿Cómo ha sido posible?
Todo se debe a una afortunada circunstancia: antes de que se incendiara, José María Avrial, pintor paisajista y escenógrafo, miembro de la Real Academia de Bellas Artes de San Fernando, que entonces ocupaba el cargo de Director de la Escuela de Nobles Artes de Segovia, además de dibujar los alzados de numerosos edificios segovianos, 
había realizado unos minuciosos levantamientos de varios de los artesonados del Alcázar, gracias a los cuales se pudo recuperar una imagen muy fiel a la que tuvo originalmente. 




Algunos son réplicas realizadas en escayola y policromadas siguiendo los dibujos de Avrial
La última techumbre recuperada recientemente, ha sido la de la Sala de la Galera, ésta, realizada como auténtica obra de carpintería
Hay dos más de madera, pero traídas de otros lugares, concretamente la que cubre la Sala del Solio, que curiosamente es del mismo autor que en su día hizo la original, un tal Xadel Alcalde, por lo que no es de extrañar su enorme parecido, 
mientras que la otra, traída de alguna iglesia castellana, cubre la capilla, cuya nave sin duda era de mayores dimensiones, a juzgar por la comprometida adaptación realizada.
en Segovia se han conservado más ejemplos de esta carpintería, como por ejemplo, la techumbre del refectorio del convento del Parral, una mejor foto de este artesonado se puede disfrutar en la exposición de José Manuel Ballester
o este pequeño ejemplo en la iglesia de San Lorenzo, 
y no podemos olvidar de tantos techos policromados que han conseguido llegar a nuestros días en casas del casco histórico, varios de los cuales compiten en la atracción del turista con los tradicionales asados segovianos.
Y tampoco tenemos que irnos lejos, basta que alcemos la vista, para disfrutar de la que cubre la nave de esta antigua capilla
Como antes he mencionado, la armadura de la Sala del Solio la hizo un tal Xadel Alcalde, cuyo nombre se supone musulmán. Ahora bien, que fuera musulmán o cristiano nos aclara muy poco sobre los orígenes. Hacerse musulmán era muy simple, bastaba decir públicamente “No hay más Dios que Dios y Mahoma es su profeta” para serlo de por vida, pero aprender el oficio de carpintero ya no es tan simple, el conocimiento del oficio tan sólo se adquiere con largos años de práctica, y se heredaba de padres a hijos.
Al comienzo de la invasión tampoco era obligada la conversión al Islam, Incluso se ofrecían la posibilidad de mantener su religión, cristiana o judía, con la única condición de pagar un impuesto.
Además, al pueblo llano, le resultaba más ventajoso el nuevo orden social, que el sometimiento al señor feudal, del que más que siervos, casi eran esclavos.
Con el nuevo orden social se fomentó el comercio y el desarrollo de las artesanías como modo de vida libre. 
Afortunadamente, aunque antes decía que nada teníamos que nos hablara de los carpinteros antes de la llegada de los musulmanes a España, estaba olvidando un importante texto que menciona carpinteros y sus obras. No es mucho, pero ya es algo, que al menos confirma históricamente, que en nuestro territorio, antes de que llegaran los musulmanes, ya existían carpinteros que techaban los edificios.
La techumbre de Teruel, tal vez sea la más antigua que conservamos, y según cuenta la historia sus constructores fueron mudéjares, 
Pero veamos que nos dicen sus maderas, que en esta ocasión nos muestran a los carpinteros que la construyeron.
Sorprendentemente, si leemos a Carmen Bernis, experta en la historia del traje medieval, visten al modo cristiano, usan pellote, zapatos, camisas con mangas encordadas, es decir vestimenta cristiana, por otra parte, el hacha que utiliza el carpintero que está escuadrando una viga es propia de los normandos, con su doble filo especial para el escuadrado de troncos, y para mayor sorpresa, todos los representados son pelirrojos.
Muestro dos imágenes más, la primera de un carpintero marroquí y la segunda de un musulmán que pintaron los mismos pintores, sin comentarios
Por otra parte, es lógico pensar que obispo autor del encargo, no se arriesgaría encargando la techumbre de su obra a quienes nunca habían hecho algo similar en la región. Y como ocurre en nuestros días, cuando hay que hacer una obra que distinga a su promotor, se trae al técnico que sepa hacer lo que nadie es capaz en el lugar. 
Lo que si pudo ocurrir fue que los nuevos clientes tuvieran gustos diferentes y pidieran en sus encargos trabajos cuya decoración respondiera a una estética diferente, algo aparentemente fácil de cambiar si existe un modelo a copiar, pero imposible de llevar a cabo si el cambio de estética requiere una transformación radical de la técnica habitual hasta entonces empleada.
Para que este cambio pudiera producirse era imprescindible que en nuestra península siguiera viva una tradición carpintera basada en un amplio conocimiento de la geometría, como la que también se realizaba en el norte de Europa.
Donde por cierto los carpinteros demostraban ser expertos. En esta armadura de la Sala Capitular de Canterbury, su armazón estructural está perfectamente integrada en una determinada traza geométrica,
Traza que, curiosamente, también incluye estrellas de ocho puntas, no totalmente iguales a las que se realizaron en nuestra carpintería, pero cuya integración en los elementos que constituyen la estructura, plantean el mismo problema técnico de nuestra carpintería de lazo.
Más tarde, cuando se afianzaba el Renacimiento, si el cliente lo exigía, nuestros carpinteros, no tenían ningún problema en cambiar la decoración, pero la técnica constructiva seguía siendo exactamente la misma, como ya mostré antes en la techumbre de Otero de Sanabria.
Y por mucho que se impusieran las corrientes renacentistas, los nuevos tratados nada explicaban sobre la forma de realizar las armaduras de cubierta, y a nuestros carpinteros nada les preocupaba seguir usando la carpintería de lazo, mezclada con la más ortodoxa construcción renacentista
La primera pista sobre las similitudes entre nuestra carpintería medieval y la europea, me la dio un texto inglés de principios del siglo XX, donde se explicaba el uso de la escuadra de pares.
Aunque en los años ochenta del pasado siglo XX no estaba seguro de que esa escuadra siguiera existiendo, no fue nada difícil encontrar una en Londres
Y quedé enormemente sorprendido al ver que el pequeño folleto que acompañaba la escuadra, también contenía las mismas antiguas recetas y reglas que Diego López de Arenas intentaba explicar en su confusa prosa de principios del XVII, 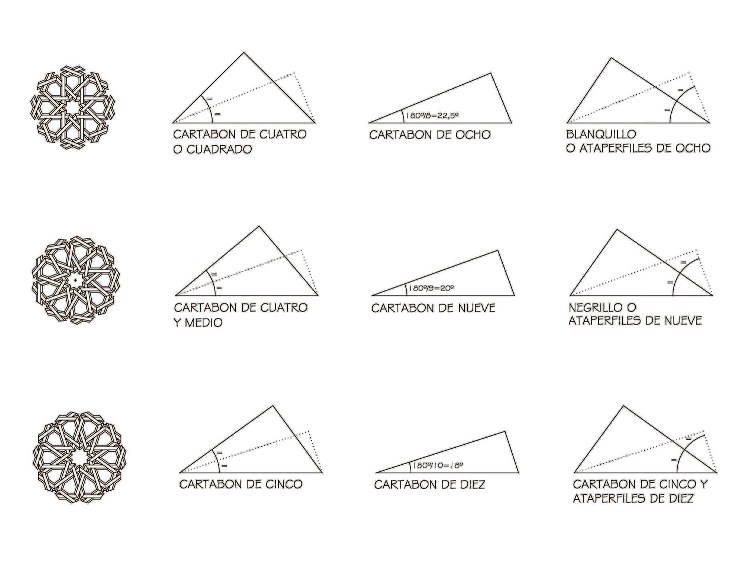
Incluso también se explica la forma de conseguir con esa escuadra los ángulos precisos para formar polígonos, algo muy similar a los cartabones que el carpintero medieval utilizaba para trazar sus ruedas de lazo.
Y ya que he mencionado los cartabones, también quiero exponer que su empleo no creo que se lo debamos a los musulmanes. Mi primer artículo referido a nuestra carpintería histórica lo debo al Dr. Christian Ewert, precisamente por el interés que mostró en saber como se podían emplear los cartabones descritos por López de Arenas en los trazados geométricos de origen islámico.
Entonces no se me ocurrió pensar como podía ser posible que. uno de los mayores expertos en el arte islámico occidental. desconociera el uso de los cartabones, pero hoy tengo muy claro que se debía a que era un procedimiento inusual en el mundo islámico, cuyos artesanos realizaban sus trazados usando exclusivamente la regla y el compás, o simples pautas cuadriculadas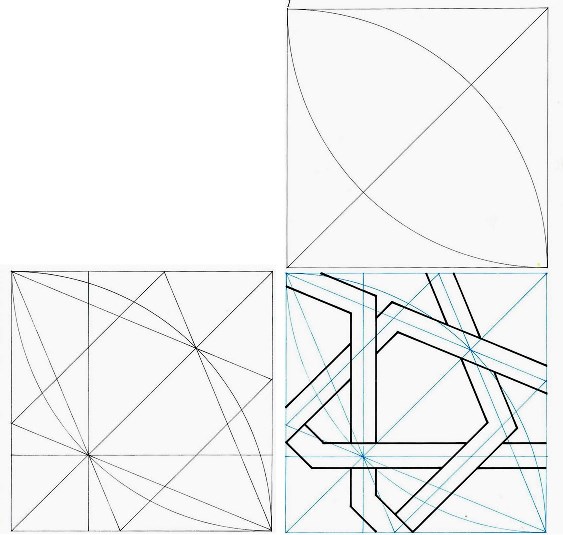
Por aquellas fechas AndreePaccard, decorador francés que trabajó durante varios años para el rey de Marruecos, 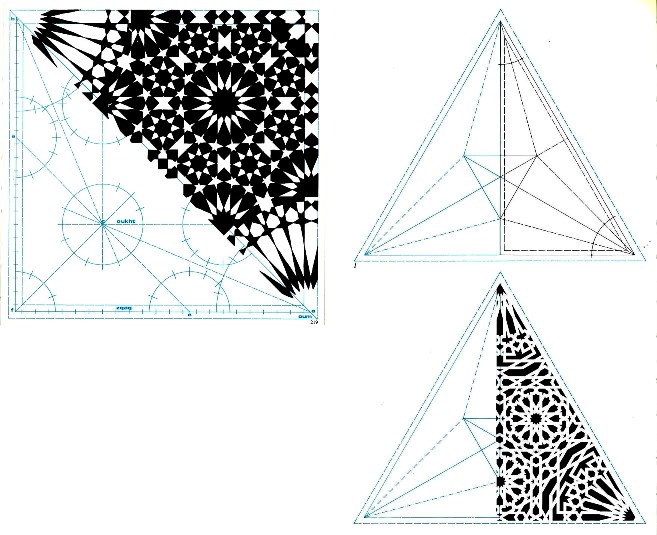 recogió en su libro sobre la artesanía marroquí varias formas de realizar los trazados geométricos,
recogió en su libro sobre la artesanía marroquí varias formas de realizar los trazados geométricos, 
incluso reproducciones de los cuadernos usados por los maestros carpinteros, que realizaban trazados de lacería en sus techumbres, en los que casi todos sus modelos geométricos se dibujaban con la ayuda del papel cuadriculado de sus cuadernos.
Los artesanos marroquíes aun siguen realizando este tipo de carpinterías, y en vez de nuestros antiguos cartabones utilizan sólo la regla, el compás, y la escuadra.
Nuestros carpinteros, al ser también expertos en geometría, habían encontrado una forma de controlar sus trazados con el uso exclusivo de sus cartabones de lazo. Veamos rápidamente como se puede trazar la rueda de nueve. No es imprescindible seguir el mismo orden, el resultado final será el mismo
En el punto que escojo como centro de la rueda, coloco un vértice del cartabón de nueve
Y donde corta a la cinta superior coloco dos colas del cartabón de cuatro y medio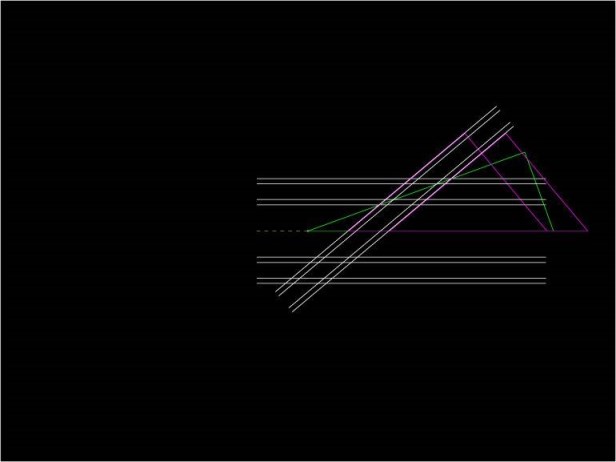
Que definen la posición de una de las cintas inclinadas
La cabeza del cartabón de nueve, colocada en la intersección que se acaba de producir, define un punto en el eje de la calle
Donde coloco la cabeza del cartabón ataperfiles
Y en las intersecciones de éste con la cinta superior, coloco dos cabezas de nueve
Que definen una de las aspillas
La otra podemos obtenerla invirtiendo loa dos cartabones de nueve
Y una vez que he definido la posición de las aspillas trazo todas las intersecciones 
Y elimino lo que sobra. Ya se ha producido la continuidad de las cintas de la aspilla con las dos horizontales
Para hacer la otra cinta inclinada puedo colocar dos cartabones de cuatro y medio en la intersección de la primera que dibujé con el eje de la calle
Y el dibujo de la cinta es inmediato
Voy a rematar los extremos izquierdos de las dos cintas inclinadas
Cortándolas con con las dos colas de nueve que pasan por el centro de la rueda
Voy a definir el encuentro de las dos cintas inclinadas ayudándome de dos trazos auxiliares
Y decido cual de las dos cintas simulará que pasará por encima de la otra, que lógicamente quedará interrumpida. El papel de los gramiles es el de acentuar este efecto de entrelazo de las cintas
A continuación preparo el siguiente cruce de cintas
Por el momento sólo estoy pensando en la pieza horizontal inferior que da continuidad a la aspilla
Dado que el resto de líneas no son necesarias
Trazo dos nuevas líneas auxiliares para dibujar el encuentro de la cinta inclinada con la cinta superior
Y elimino lo que sobra, y ha quedado definida la haliba, que es el taujel cuya forma recuerda la del halibut, pez cuyo hábitat meridional se encuentra en el Canal de la Mancha, lo que nos vuelve a relacionar esta carpintería con las gentes del norte del Atlántico.
Para buscar el límite izquierdo de la cinta superior utilizo dos colas del cartabón de cuatro y medio que pasen por los extremos de la boquilla del sino, que es como se llama el pequeño taujel que se interrumpe en la haliba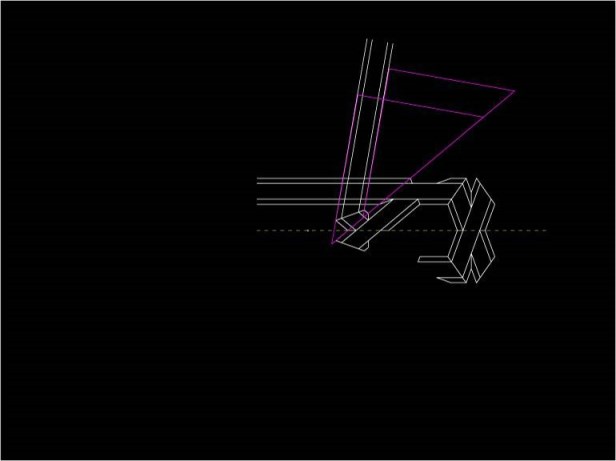
Y con su ayuda trazo una nueva cinta, que no necesita nada más que para delimitar la pieza cuyo nombre es el costadillo del azafate.
me permiten definir ese encuentro
Del que elimino todas las líneas sobrantes, y ya tengo todas las piezas que componen una rueda. Tan sólo salen cinco diferentes, las dos medias aspillas son idénticas entre sí e iguales l pequeño taujel de la cinta inferior
Para dibujar la rueda completa, tan sólo tendré que repetir este proceso, girando 40º cada conjunto. Previamente elimino los trazos de los extremos que se repetirían.
Y ya tenemos completa la rueda de nueve brazos.
Un exhaustivo trabajo del alemán GerdSchnaider, quien ha recogido cientos de trazados realizados en la Turquía Seleucida entre los siglos X al XII,
Nos muestra que allí se desarrolló hasta límites inimaginables el uso de la decoración geométrica, aplicada a la arquitectura
Sobre todo en las portadas de las caravanserías, donde paraban las caravanas que sustentaban una importante parte del comercio que se practicaba en el mundo islámico
Y de alguna forma, esas caravanas acabaron trayendo dichos patrones a la Granad nazarí, algunos de los cuales son perfectamente asimilables a los que realizaron nuestros carpinteros.
Pero en general, los motivos seleucidas tienen una libertad compositiva inexistente en nuestra carpintería de lazo
Tal vez, donde encontramos por primera vez semejantes motivos geométricos en nuestra península, sea en la sinagoga toledana conocida como Santa María la Blanca
Es muy lógico pensar que los motivos decorativos tan populares en el arte celta, requerían una importante práctica de la geometría, algo indispensable para llevar acabo sus complejas composiciones
Así como que estuvieran acostumbrados a la decoración formada por cintas entrelazadas
Como las que también llevaban a cabo en tantos de sus trabajos, fuera en el material que fuera.
Algo que también era familiar en el mundo vikingo o escandinavo
No es de extrañar que carpinteros de herencia celta o visigoda, (en esta caso, ya convertidos en musulmanes del reino nazarí), con amplia experiencia geométrica, acogieran con agrado estas nuevas decoraciones, y fueran capaces de adaptarlas a sus trabajos, primero a simples falsos techos, y más tarde atreviéndose a soluciones más complejas
Una de las ventajas de la carpintería basada en estos trazados geométricos, es que proporcionaba al carpintero un fácil control sobre las medidas de los distintos paños que componían sus techos, lo que posibilitó su prefabricación. Esto hizo que el sistema perdurara siglo tras siglo.
Para dar una idea de cómo se pueden controlar con precisión las medidas de todos los elementos que componen un conjunto, la techumbre del salón del trono del palacio de Comares, puede ayudarnos enormemente.
Puede ser difícil de creer, pero el proceso utilizado al dibujar cualquier rueda de lazo, permite al carpintero detectar cualquier error que cometa, lo que hace que las medidas del conjunto final sean exactas sin necesidad de comprobaciones finales.
Siguiendo una sencilla regla, las medidas de la rueda de ocho siempre saldrán idénticas para un determinado ancho de sus cintas, y lógicamente, esa primera rueda controla las medidas del resto del trazado que deriva directa y exclusivamente de ella.
Para realizar la techumbre anterior, sin cometer errores, basta con saber trazar la rueda de ocho que aparece en este dibujo, y los fragmentos de ruedas de dieciséis que dicha rueda desculata.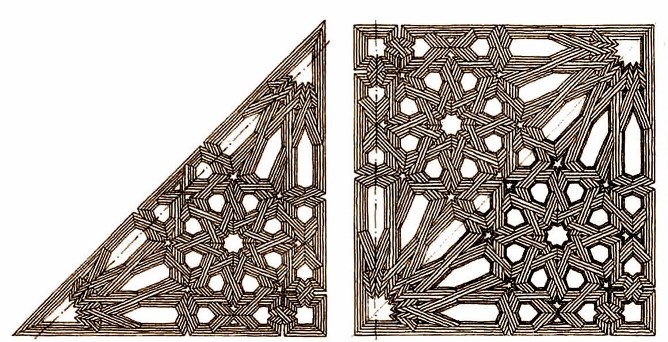
Girando el triángulo anterior sobre si mismo, se convierte en un cuadrado
Y volviendo a girar el cuadrado obtenido sobre si mismo, se obtiene el rectángulo de la derecha
Nada más fácil que conseguir el cuadrado de la derecha a partir del rectángulo anterior. Y ya tenemos el motivo con el que se compondrá todo el artesonado del Salón de Comares
Estas son las variantes realizadas a partir del módulo anterior, modificando solamente su zona central lo que mantiene los bordes de todas las composiciones exactamente idénticos, algo indispensable para formar con ellos un conjunto más complejo.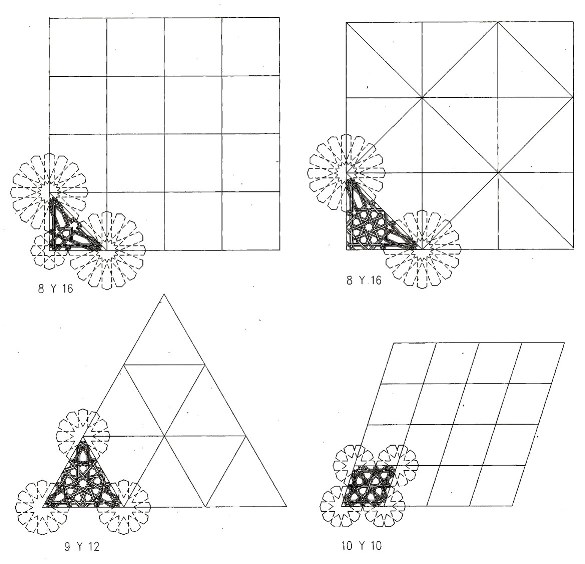
Los carpinteros castellanos tan sólo utilizaron estos cuatro patrones para llevar a cabo cualquiera de sus trabajos, y basta saber como se traza la rueda del que depende cada uno, para poder realizar cualquier trazado sin miedo a equivocarse.
Al principio de esta charla mostré como, a partir de una única pieza, se puede deducir parte del conjunto al que perteneció. Y para terminar, acabaré con otro ejemplo en el que me facilitaron estos dos fragmentos, pertenecientes a la sala principal de una casa nazarí del Albayzin granadino.
En esta ocasión quien los encontró. fue Carlos Sánchez, arquitecto que estaba restaurando su propia vivienda, y que sabedor que yo me encontraba recomponiendo una serie de artesonados para el que iba a ser el nuevo Museo Nacional de Arte Hispanomusulmán de la Alhambra, se presentó para ver si de ellos podía deducirle como pudo haber sido el techo del que procedían.
En realidad, aunque pueda parecer increíble, en principio bastó esta única pieza para empezar a desvelar el trazado original.
Había que establecer algunas hipótesis, por ejemplo, que el clavo que aparece en la ranura inferior se hubiera colocado en su eje central, como solía ser habitual, medio oculto en la ranura, para que pasara desapercibido, lo que permitía suponer el ancho real de la pieza. Otra hipótesis sin confirmar era que el trazado se hubiera hecho a calle y cuerda, es decir, que la separación entre cintas fuera igual al doble del ancho de la cinta, algo también habitual en los techos nazaríes
Lo que ya no eran hipótesis, sino evidencias por los cortes de sus extremos, es que la pieza se cruzaba en el izquierdo con otra a noventa grados, y en el derecho con una a treinta grados. (en la foto no se aprecia la trasera de la pieza, con el mencionado corte a 30º)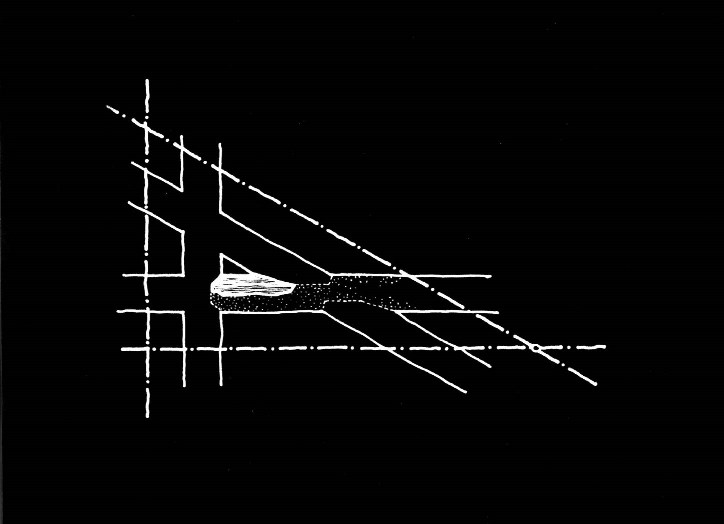
El primer trabajo consiste en tratar de encajar el fragmento encontrado en una trama que cumpla las condiciones de los cortes descritos anteriormente.
El dibujo se compone del fragmento encontrado, y punteado he dibujado el resto de la pieza, deducido de las consideraciones anteriores. Luego he trazado cintas que se cruzan con la pieza según los ángulos de sus extremos, y he imaginado los ejes de las calles que se compondrían con las cintas representadas en el dibujo.
Podría pensarse que me he adelantado al suponer cuales eran las calles a las que pertenecen las tres cintas del dibujo, pero analizando todas las posibilidades, se llega a las siguientes conclusiones:
El eje vertical sólo puede estar a la izquierda de la cinta vertical, dado que si estuviera a la derecha la cinta estaría interrumpida por un cruce existente.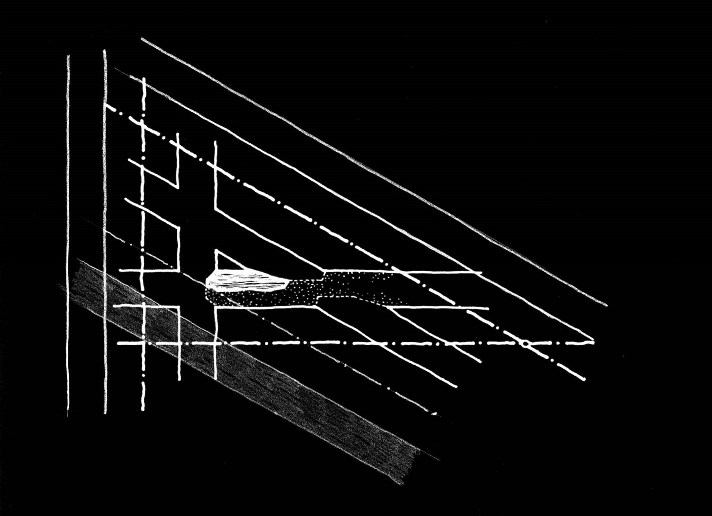
Hacemos lo mismo para la pareja de la pieza que cruza a 30º y confirmamos que sólo es posible lo planteado inicialmente
Finalmente intentamos buscar una alternativa horizontal a la pareja de la pieza encontrada y vemos que tampoco es posible una solución distinta de la planteada.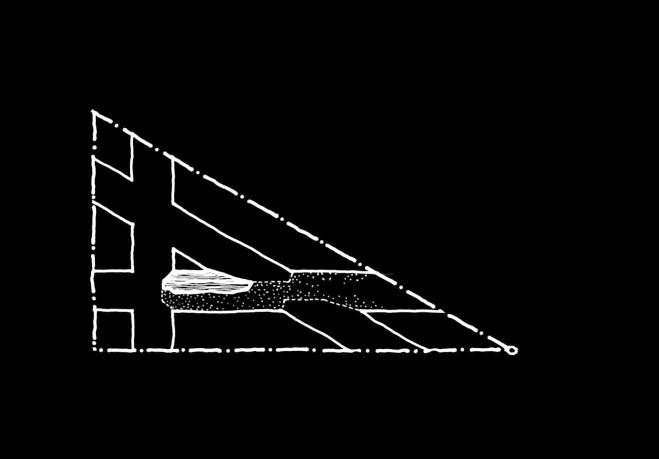
Eliminadas las hipótesis anteriores queda confirmado que la pieza forma parte de un trazado del que por el momento sólo conocemos lo comprendido en este triángulo, 
es lógico pensar que a partir del eje horizontal se producirá una simetría. Podría haber utilizado cualquiera de los otros ejes, después comprobaremos que habría sido indiferente
A partir del trazado anterior no se necesita mucha imaginación para completar cualquiera de las dos figuras que aquí muestro, en las que cabe la duda sobre la solución de las cintas que se cruzan a noventa grados.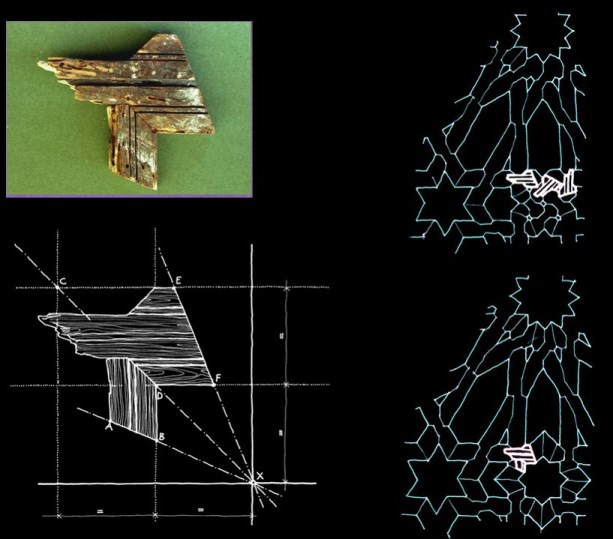
Pero afortunadamente, pasado algo más de un mes desde que aparecieron las primeras piezas, el arquitecto de la obra encontró entre los escombros estas dos nuevas piezas, que tenían toda la apariencia de haber estado colocadas juntas. Como en el caso de las dos primeras encontradas, una sólo confirmaba las hipótesis manejadas, aunque la pequeña servía para corroborarlo
1º El gramil donde se encontraba el clavo era efectivamente el central de la pieza y por tanto la primera suposición sobre su ancho era correcta.
2º Los cortes convergentes tanto de la pieza mayor, como del borde de la otra pieza se unen en un único punto que resulta ser el eje de las calles que se cruzan a 90º en ese punto, lo que confirmaba que la calle (separación entre dos cintas) era exactamente el doble del ancho de las cintas.
3º Y finalmente de las dos opciones posibles para las cintas que se cruzaban a 90 grados, quedaba la estrella de ocho puntas como única admisible.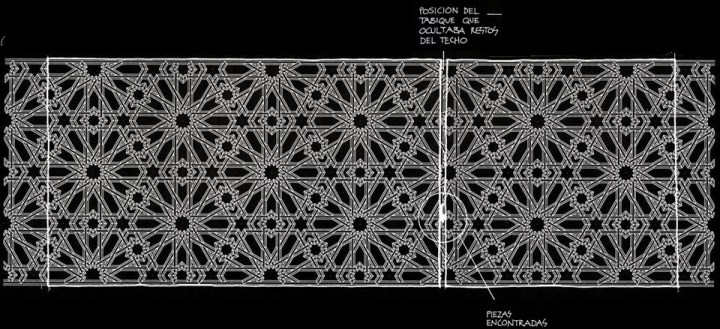
Desarrollado el dibujo a partir de los módulos exagonales obtenidos, y rematados los bordes longitudinales con las medias calles que suelen completar este tipo de trazados, la anchura del conjunto coincidía exactamente con la de la habitación en la que se habían encontrado las piezas.
Como la posición del tabique que había protegido estas piezas de un fuego sufrido, del que aun quedaban señales claras, eran perfectamente conocidas, bastaba mover de derecha a izquierda el dibujo del conjunto para situar las piezas encontradas la posición que ocupaba el tabique. Lógicamente podían situarse de varias formas, pero en una de ellas el conjunto quedaba perfectamente centrado entre las dos paredes extremas, lo que animó mucho a pensar que las hipótesis manejadas se acercaban a la realidad desconocida.
El siguiente paso fue reconstruir lo averiguado. Era muy posible que los espacios entre cintas, estrellas o azafates, estuvieran policromados o tallados, pero como nada se encontró que permitiera recomponer estos últimos, la reconstrucción se paró evitando inventar nada, dejando el lugar de sinos y azafates en una tinta neutra que armonizara con la madera de los taujeles, nombre genérico que reciben las piezas que componen las cintas.