Buenos días, es una tradición de la Academia que quienes formamos parte de ella hablemos de la obra que entregamos al ingresar, y hoy me ha tocado a mi hablar de estos dibujos que representan sendas armaduras de lacería.
¿Y que puedo decir de estos dibujos?
Poca cosa:
En principio, que están hechos sobre papel vegetal y con tinta negra y sepia.
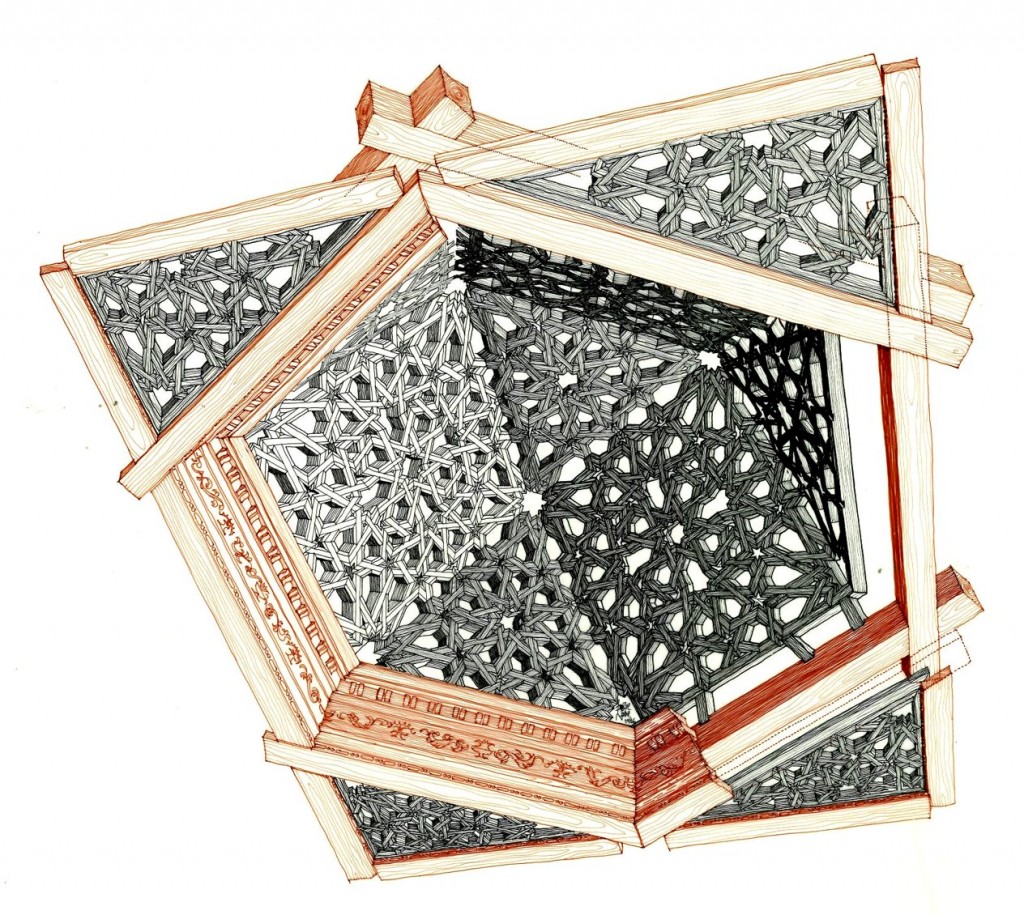
Ésta primera representa el artesonado de la capilla de la Virgen del Castillo, en la iglesia de san Facundo y san Primitivo, en Cisneros, provincia de Palencia,
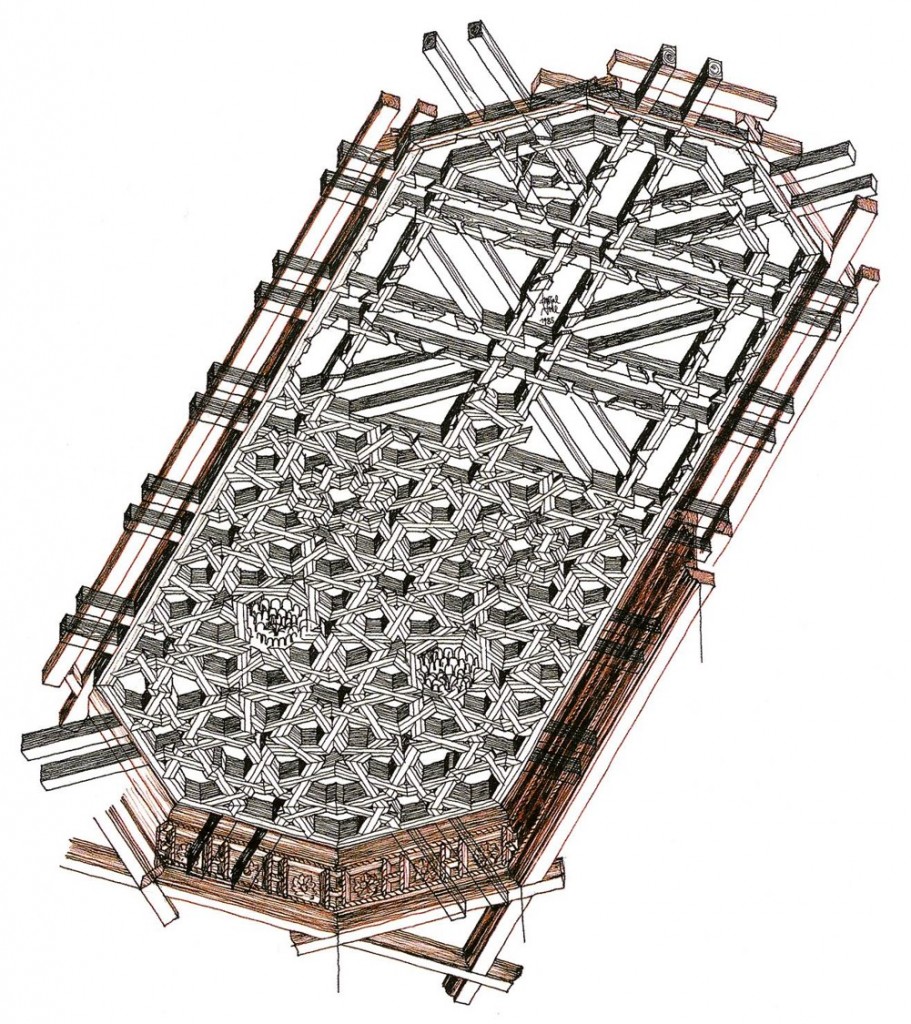
Y ésta otra, el curioso artesonado de una capilla lateral de la iglesia de Santiago en Granada.
Ambos son perspectivas cónicas, y tratan de explicar como se organizaban estos techos, y son parte de las ilustraciones de mi libro sobre la carpintería de armar española.
Y no se me ocurre nada más
Pero como supongo que con estos comentarios no habré cumplido con el compromiso adquirido, contaré cómo me vi metido en semejante lío de tener que representar unos techos tan complejos, en vez de dibujar un paisaje. (Lógicamente no son los únicos dibujos de este libro)
En muchas ocasiones, las fotografías que se pueden hacer para mostrar determinado conjunto carpintero, apenas explican nada del mismo. Hay que reinterpretarlas
Y eso sólo es posible haciendo un dibujo que seleccione de las fotografías realizadas lo que realmente interesa, eliminando parcialmente las partes que quedan suficientemente explícitas para poder ver lo que ocultan.
Desafortunadamente, no siempre podemos hacer buenas fotos, y tenernos que conformarnos con la imagen que las circunstancias permitieron, y cuando ocurre, como en este caso, que la calidad de la foto no era suficientemente buena para la publicación,
Al menos nos sirve para hacer un dibujo, en el que además podamos mostrar los elementos de la estructura que en la foto nunca pueden verse, así como la descomposición de sus elementos, o lo que consideremos conveniente.
Y así, por unas u otras razones, el libro se va llenando de dibujos, como éste de una de las capillas laterales de la iglesia de Erustes, en la provincia de Toledo
O la armadura de la iglesia de San Andrés de Zamora, una atrevida solución que cubre una planta de unos cuatrocientos metros cuadrados sin ningún tipo de soporte intermedio
O esta seisavada, que el papa Luna mandó construir en su castillo de Mesones de Isuela
O la que tuve que recomponer a partir de los fragmentos conservados en la iglesia granadina de san Jerónimo, para el que iba a haber sido Museo Nacional de Arte Hispanomusulmán
O este lujoso artesonado, que mandaron levantar los Reyes Católicos en la Aljafería de Zaragoza, para su salón del trono
O la curiosa pechina del presbiterio de la iglesia del convento de la Madre de Dios en Sevilla
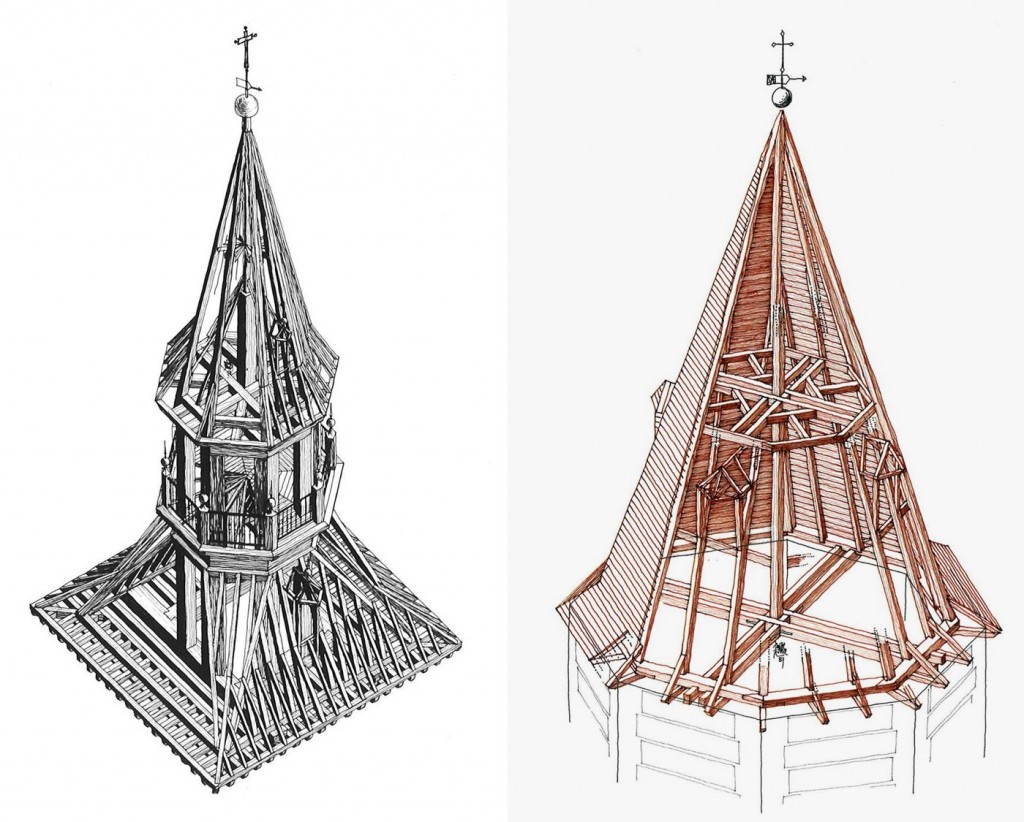
O estos dos chapiteles, el de la izquierda de la iglesia de San Sebastián de Méntrida en la provincia de Toledo, y el de la derecha, uno de los rehechos tras el incendio sufrido en el Alcázar de Segovia
O este rico artesonado renacentista de Otero de Sanabria, una pequeña aldea perdida en la provincia de Zamora
O éste también renacentista de los Reales Alcázares de Sevilla, etc. etc.
Entre dibujos y fotografías, el libro cuenta con 500 ilustraciones,
Sin contar las que aparecen en las 123 páginas del léxico carpintero con que se completa el volumen.
Como ya he dicho, estos dibujos se hicieron para un libro, pero no he explicado que hasta cumplidos los cuarenta años jamás se me había pasado por la mente la idea de estudiar nuestra carpintería histórica, ni sabía nada de ella.
Yo era un arquitecto de tantos que hacía edificios de viviendas,
Principalmente en Madrid
o apartamentos turísticos,
También urbanizaciones
o naves industriales
Precisamente uno de mis primeros trabajos fue una fábrica de ataúdes, y hablando de arquitecturas fúnebres, también me tocó hacer un panteón, eso sí, muy bien impermeabilizado, porque el cliente quería no tener goteras durante toda su muerte.
Y es que los arquitectos, sobre todo los que ya tenemos un porrón de años, salíamos de la escuela como especialistas en la totalidad, lo mismo teníamos que saber urbanizar una ciudad entera, hacer un hospital o un teatro de ópera, pongo por caso, y por supuesto calcular su estructura y sus instalaciones, aunque eso sí, en la asignatura de instalaciones aun nos enseñaban los timbres de las viviendas que funcionaban con una pila consistente en un frasco cilíndrico de vidrio con un electrolito y los correspondientes ánodo y cátodo, a pesar de que habían dejado de existir antes de nuestra guerra civil. En una rehabilitación en Burgos encontré uno y me hizo una enorme ilusión.
Y lógicamente, cuando nos hacían un nuevo encargo, si era algo que nunca habíamos hecho, había que empezar a comprar libros y estudiar el tema hasta saber lo mínimo para enfrentarnos al trabajo.
Y eso es lo que tuve que hacer con un peculiar encargo para recomponer y montar los fragmentos de unos artesonados de lo que llamaban carpintería mudéjar en los nuevos museos que se acababan de levantar junto a la Alhambra, en los terrenos del Generalife.
La mayoría de las piezas se encontraban almacenadas en sótanos, en fragmentos más o menos destrozados
Y una vez que recibí el encargo del trabajo, por mis manos pasaron fragmentos y fragmentos de armaduras, algunas en razonable buen estado, que poco a poco se iban montando en los nuevos museos
Pero realmente aquel encargo no tenía nada en común con el resto de los que hasta entonces había realizado.
Por esas casualidades que alteran el curso normal de nuestras vidas, la hija de don Manuel Gómez-Moreno, poco tiempo antes de que se desencadenase esta historia, me acababa de regalar un facsímil de un manuscrito sobre carpintería histórica que había publicado su padre unos pocos años antes, su título:
Primera y sigunda parte de las reglas de la carpintería hecho por Diego López de Arenas en este año de mil seiscientos diecinueve.
Es algo complicado explicar la serie de circunstancias que hicieron que pasara todo un mes de agosto en el que lo único que hacía era tratar de entender el manuscrito, con la ayuda de cientos de dibujos en los que concretaba las palabras leídas y releídas, hasta estar seguro de que lo que interpretaba tenía algún sentido, y sorprendentemente, al final del mes todo el manuscrito de López de Arenas ya me resultaba inteligible.
Pensé que tras todo el esfuerzo realizado, el trabajo merecía ser publicado, pero al ser yo ajeno al ámbito universitario, o al de la investigación histórica, no tenía ni idea de cómo poderlo publicar, y sorprendentemente, cuando ya pensaba olvidarme del tema, por otra serie de casualidades, El Dr. Ewert me pidió un artículo para Madrider Mitteilungen, la revista que edita el Instituto Arqueológico alemán para las aportaciones de sus institutos en el extranjero.
Casualmente ese mismo otoño, el Colegio de Arquitectos convocó por primera vez un premio de investigación, al que presenté el trabajo, con la esperanza de conseguir su publicación, pero a pesar de conseguir el premio, en el presupuesto del Colegio no había prevista ninguna partida que lo permitiera.
Sin embargo, se debió producir la conjunción de Júpiter con Saturno, en el plano de la órbita de Venus, o algo aun más complicado, pues en el mes de enero el Ministerio de Cultura, por primera vez en su historia convocó el Premio Nacional de Artesanía Marqués de Lozoya, ocasión que aproveché y que afortunadamente también gané, y al menos, ese premio sí llevaba implícita la publicación del trabajo.
para no ser pesado, y resumiendo, en dos o tres años pasé de no haber oído hablar de carpintería mudéjar, a convertirme en su principal especialista, al haber logrado comprender todos los secretos del oficio, que ciertamente no eran tales secretos, pero sí difíciles de entender para alguien que no reuniera los conocimientos de un arquitecto, que no tuviera experiencia en trabajar la madera, y que no dominara el dibujo, ni la geometría, o la trigonometría.
Y además de reunir las condiciones antedichas, era imprescindible disponer del mencionado manuscrito, del que sólo se había hecho una edición de 500 ejemplares, la mayoría regalados a personas que, o eran simples bibliófilos, o que el tema, por ser demasiado técnico, no les interesaba.
Lo que me animó a seguir investigando, buscando ejemplos de esta carpintería por toda España,
Con tal motivo, convencí al Ministerio de Cultura, para realizar las Bases para formar un inventario de armaduras de lacería, descubriendo cientos de ellas repartidas, sobre todo, por los territorios que fueron del reino de Castilla, y sacando a relucir miles de armaduras que en España se habían realizado para quedar vistas.
Desafortunadamente, su terminación coincidió con las transferencias de competencias del Ministerio de Cultura, lo que complicó la continuidad del trabajo, y el inventario final que estaba diseñado para llevarlo a cabo por provincias, se quedó en las estanterías del IPHE, dado que cada Comunidad Autónoma no quiso saber nada de él, al querer zafarse del tradicional centralismo al que consideraban que habían estado sometidas.
Ese inventario precisaba un libro en el que estudiar nuestra carpintería histórica, tema que sorprendentemente estaba prácticamente inédito, y para poder explicar cada solución carpintera que iba encontrando, eran necesarios dibujos y fotografías.
Las fotografías en principio eran más fáciles de realizar, pero solían dejar muchas partes de la obra carpintera oculta, de ahí que los dibujos fueran un complemento imprescindible.
Cuando se contemplan muchos de estos dibujos, como el que aquí pongo de ejemplo, inmediatamente se piensa que el trabajo de carpintería representado debía ser algo sumamente complicado de llevar a cabo, y sin embrago, su aparente complejidad de trazado, era lo que paradójicamente permitía la fácil realización de esta carpintería.
Pero para poder entender lo que acabo de afirmar, hace falta comprender la geometría que la hace posible, y para ello debemos regresar unos siglos en la historia, al menos hasta el entorno del XI y XII, y viajar hasta lo que conocemos como Asia Menor en tiempo de los Seleucidas, donde surgieron todo tipo de trazados geométricos, allí se puede encontrar cualquiera que hoy seamos capaces de imaginar, empleados principalmente como decoración de las obras de arquitectura.
La circunstancia de que por su territorio pasaran las rutas provinentes de Asia, facilitó que el comercio de las caravanas acabara siendo el vehículo que con toda probabilidad hizo llegar a nuestro país tales motivos geométricos.
Motivos que formaban una importante faceta de su arquitectura, con independencia del material empleado. En la madraza de Konya por ejemplo, aparecen las ruedas de lazo que después constituirán el principal motivo de la decoración geométrica que llegaría a la Granada nazarí y posteriormente a nuestra carpintería, si bien en este caso, era la cerámica el material soporte de esta decoración.
Piedra o madera también permitían el desarrollo de este tipo de decoración geométrica.
En algún momento, tal vez en el entorno de los siglos XIII y XIV estos motivos geométricos irrumpen en los palacios del recinto de la Alhambra nazarí, aquí representada por mi buen amigo Miguel Sobrino.
Arraigando con tal fuerza, que tan sólo en la Torre de Comares encontramos un rico muestrario de techos de madera realizados con esta técnica geométrica
Y ahora es oportuno hacer un inciso para mencionar que en le siglo XIV Muhamad V estaba ampliando sus palacios de la Alhambra, mientras Pedro I de Castilla hacía lo mismo en los Reales Alcázares sevillanos. Con tal motivo nos consta que se intercambiaron operarios
No dudo que si un carpintero del rey D. Pedro llegó a la Alhambra quedaría deslumbrado por los magníficos techos que engalanaban todos los palacios existentes en el recinto, especialmente el conjunto de la Torre de Comares
Lo más sorprendente es que un carpintero nazarí, en pocos minutos, pudo haber explicado al castellano la sencilla forma de diseñar un techo aparentemente tan complejo, como el que aquí muestro de la Alcoba Real del Salón de Comares
Pero antes, imaginemos que quisiéramos hacer uno similar, tal como hoy acostumbramos: en primer lugar decidiríamos la pendiente de sus faldones, en función del material de cobertura, y una vez concebido el techo, procederíamos a ajustar su decoración vista. Si decidiéramos ajustar una geométrica como la que los carpinteros musulmanes hacían para la Alhambra, nos encontraríamos con una misión prácticamente imposible, pensemos por ejemplo en como se resuelven los encuentros de este techito. El juego de ruedas se ajusta exactamente al tamaño de los diferentes faldones, con los centros de sus estrellas dispuestos exactamente en los vértices o aristas de encuentro de los diferentes paños, y de esa forma la traza geométrica tiene una continuidad ininterrumpida por toda la obra.
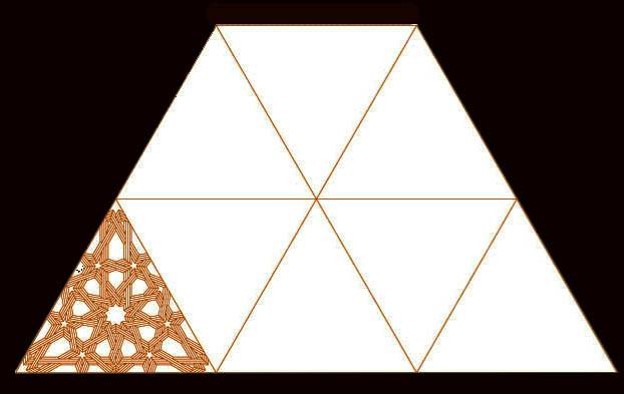
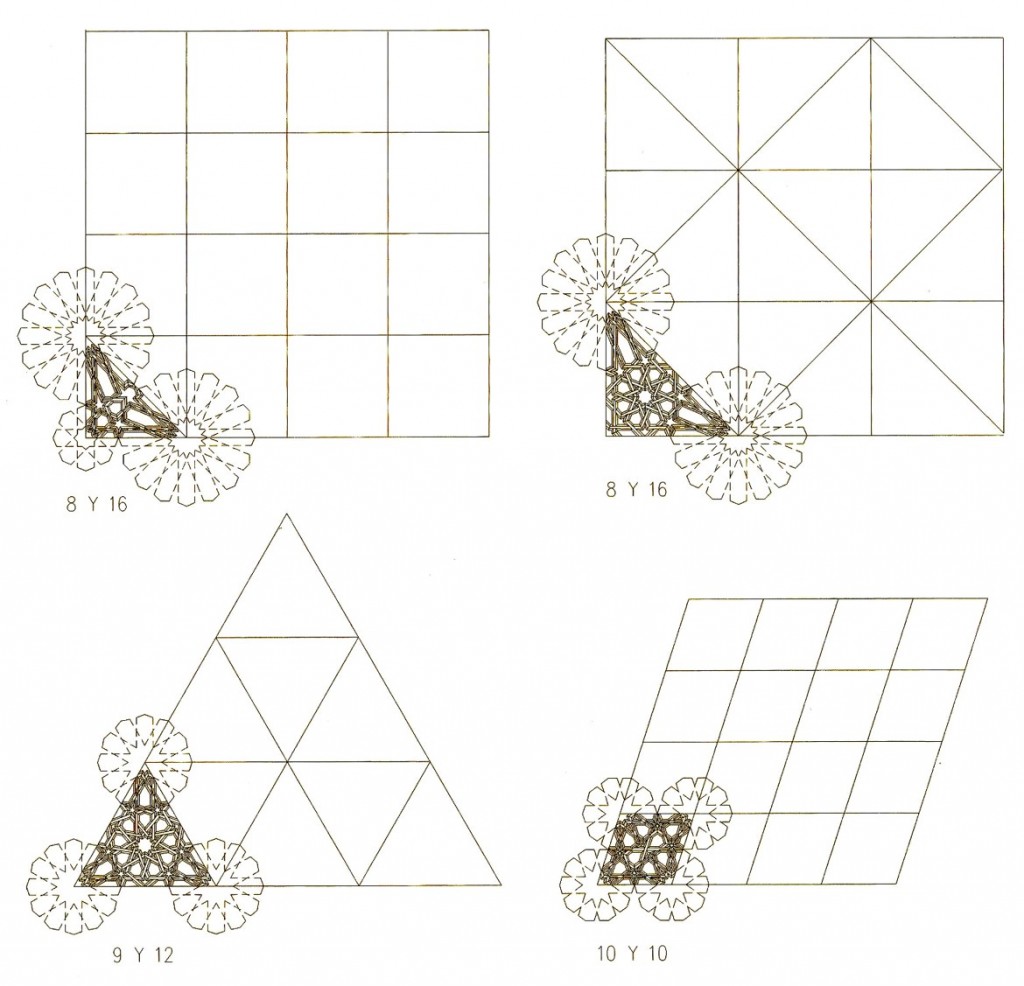
La sencilla solución de este problema es lo que sin duda fascinó a los carpinteros castellanos. El proceso de diseño es radicalmente distinto del que acabo de exponer. El carpintero granadino primero diseñaba un tablero cuyas medidas se corresponden con un determinado trazado geométrico, por ejemplo el de base triangular equilátera que aquí muestro, por supuesto con la forma trapezoidal que debe tener cualquier faldón de techo a cuatro aguas.
Todos los módulos son idénticos y llenan completamente el espacio escogido para convertirlo en un faldón del futuro techo
Realmente, el dibujo anterior estaba incompleto por su borde inferior, puesto que los módulos se rematan en ejes de calles, y hay que proporcionar la media calle que completará el borde inferior del conjunto. Este es el momento de ajustar el trabajo a las medidas del espacio a cubrir, ya que su borde inferior es el único elemento que tendrá una relación directa con la sala cubierta.
Pero hasta ahora hemos usado un módulo triangular que se adaptaba sin problemas a la forma trapezoidal del faldón escogido. ¿Qué haremos con este triángulo en la parte horizontal del techo, que forzosamente ha de ser cuadrada?
Sencillamente cortamos el módulo de partida por líneas que forman con su base ángulos de 45º, y después retocamos caprichosamente la lacería correspondiente al nuevo ángulo superior, que ahora es lógicamente de 90º.
Es evidente que nuestro nuevo diseño forma la cuarta parte del cuadrado que necesitábamos.
Ya tenemos un faldón y el almizate cuadrado. El resto de faldones serán idénticos al que aquí se muestra, y para su construcción, si el carpintero ajustó la base del faldón al lado de la alcoba, ya no precisa medir nada más, tan sólo realizar una serie de trazados geométricos que acabamos de ver dibujados.
La propia geometría del diseño condiciona el volumen que tendrá el conjunto una vez unidos todos sus elementos. Este proceso es el lógico cuando se trata de hacer un falso techo decorativo, no tanto si queremos construir una armadura de cubierta, pero es evidente que con unas pequeñas transformaciones, el sistema es aplicable a la construcción de armaduras.
Todo lo anteriormente expuesto tiene una lógica aplastante. Pero hemos dado por supuesto que sabemos realizar el trazado geométrico correspondiente a la malla triangular equilátera, y lógicamente surge una pregunta ¿No será demasiado complicado el trazado de esas figuras geométricas?
Lo más sorprendente es que los carpinteros castellanos encontraron una forma de realizar esos trazados con gran sencillez y precisión gracias a un hábil manejo de unos juegos de cartabones, los que el carpintero ya usaba para diseñar, medir y cortar sus armaduras. Pero a eso me referiré más tarde, ahora mostraré otro ejemplo más complejo.
Habíamos visto el juego que nos permitía la combinación de la rueda de nueve con la de doce, veamos ahora las posibilidades de la rueda de ocho con su desculatada de dieciséis. Para ello nada mejor que analizar el techo que cubre el Salón del trono de la Alhambra.
Aquí tenemos el motivo de partida: una rueda de ocho brazos que desculata otras dos de dieciséis, de las que tan sólo vemos tres brazos en los vértices del triángulo.
Pasar del triángulo al cuadrado no tiene mayor complicación.
Y cuatro cuadrados como el de la imagen anterior forman este gran cuadrado que será la base de la composición.
Una vez conseguido el módulo de partida hay que alterarlo a fin de conseguir variedad en el conjunto, y para ello se vacía la zona central, después se rellenará el hueco conseguido por el simple procedimiento de prolongar cintas del trazado restante.
Más variantes se pueden conseguir eliminando una zona mayor, y del mismo modo que en el caso anterior, la prolongación de las cintas de la traza restante proporcionan la base de nuevas soluciones.
El almizate horizontal se forma con el anterior módulo, al que se la alteran las cuatro esquinas cambiando las ruedas de dieciséis por ruedas de ocho con cintas dobles. El espacio central se cierra con cintas que forman un octógono donde se apoyará un cubo de mocárabes.
El faldón contiguo al almizate debe modificar sus esquinas superiores para hacerlas coincidir con las modificadas en el almizate.
En el centro bastará modificar el triángulo que corresponde a una octava parte del vacío dejado.
En el centro del faldón inmediatamente inferior encontramos esta variante
Y a su lado esta otra, en la que ya aparece la esquina superior izquierda recortada para ir formando el poliedro final.
En este módulo del centro del faldón inferior el vacío a rellenar era el menor de los realizados y en él, la rueda de dieciséis brazos se sustituye por una de ocho brazos
A su lado encontramos esta otra variante
Los cortes de los bordes son fáciles de reproducir con precisión usando como pauta la geometría del dibujo, como si de una pauta cuadriculada se tratara.
Lógicamente todo es evidente si sabemos trazar las ruedas, pero, ¿No es demasiado complejo el proceso para que pudiera ser fácilmente asimilado por los carpinteros castellanos?
Usando el trazado como pauta básica podemos reproducir sin cometer errores el corte del lateral del faldón superior
Y el del faldón intermedio, del que una parte ya estaba incluido en el módulo situado a su derecha
Y finalmente el corte lateral del faldón inferior
Colocando cada módulo en su sitio conseguimos el siguiente conjunto, al que sólo falta completar la parte derecha, simétrica de la izquierda.
La fiabilidad del levantamiento conseguido basándome exclusivamente en la geometría resultante del desarrollo de las ruedas de ocho y dieciséis brazos, es tanta que una vez compuesto el dibujo tridimensional del conjunto se pudo comparar con un levantamiento fotogramétrico realizado por Antonio Almagro, y las coincidencias fueron totales.
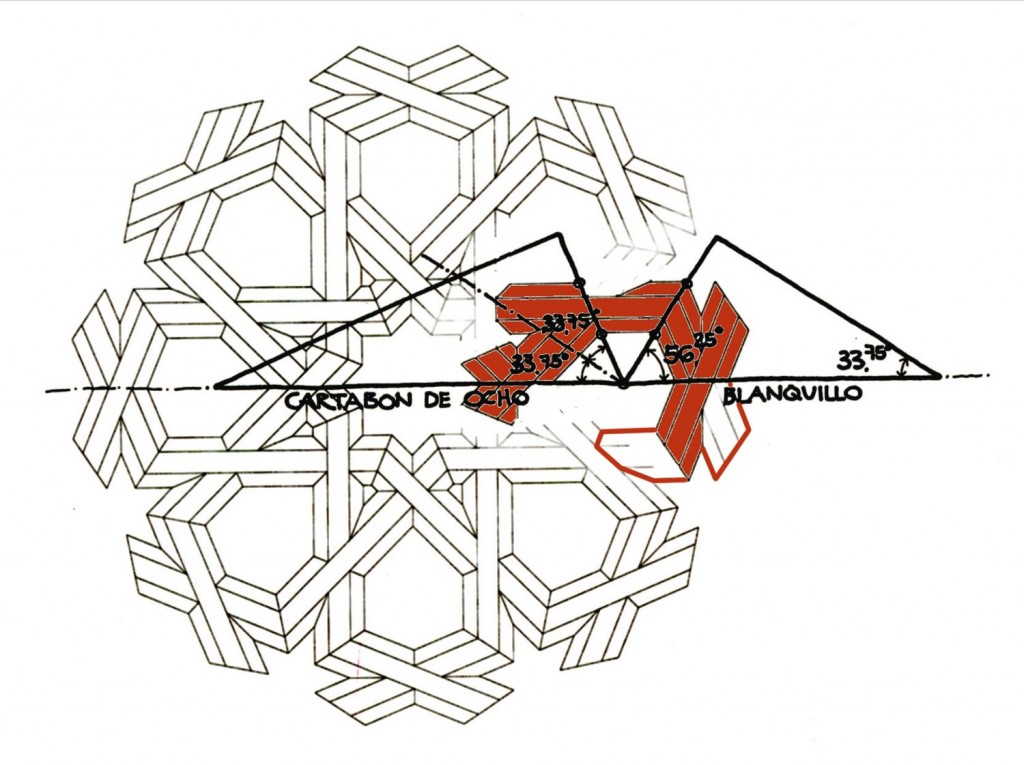
Realmente, he mencionado la sencillez con que se reproduce cualquier techumbre de lacería, pero lógicamente he dado por supuesto que sabemos trazar las ruedas de lazo de las que dependía toda la geometría del conjunto. Veremos que trazar las mencionadas ruedas tampoco es complicado, lo que los carpinteros castellanos, como antes mencioné, resolvieron con sus cartabones, similares a los que usaban para trazar y cortar sus armaduras
La rueda de lazo tiene un sencillo proceso de diseño usando los cartabones de lazo. No voy a exponer todo el sencillo proceso que se sigue, me limito a mostrar el trazo fundamental, del que depende que las ruedas sean siempre proporcionales entre sí. Se trata del que aparece en este dibujo y que corresponde a la cabeza del cartabón de ocho, que se hace pasar por el encuentro de la haliba y el costadillo, que proporciona un punto en el eje de la calle, donde se ha de colocar la cabeza del blanquillo para determinar el encuentro entre el costadillo y la media aspilla
Es importante saber que tenga la rueda los brazos que tenga, tan sólo es preciso saber trazar las cinco piezas que en ésta de ocho brazos aparecen coloreadas.
En realidad un brazo completo se compone de siete piezas, pero las dos que faltan son exactamente iguales a la media aspilla.
Y de las ruedas de lazo se derivan sus desculatadas cuyo trazado es directamente dependiente de las ruedas de origen.
En el mundo islámico, que también emplea las ruedas y sus desculatadas no se mantiene la rigidez de trazado que impusieron los carpinteros castellanos a sus trazados, imprescindible para poder controlar sus diseños.
Lo importante de los mencionados trazados básicos es su capacidad de generar mallas regulares que servirán para controlar futuras composiciones que se convertirán en paños de armaduras
Podríamos pensar que utilizar tan sólo las combinaciones anteriores daría unos diseños forzosamente de una gran monotonía, sin embargo voy a mostrar una serie de ejemplos resueltos a partir de esta pareja de ruedas para comprobar que no es así.
por ejemplo en esta armadura de Madrigal de las Altas torres, donde fue bautizada Isabel la Católica, sólo se emplea el motivo anterior como generador de todo el conjunto.
El carpintero se reserva siempre su derecho a realizar pequeñas trampas para adaptarse al espacio disponible, lo que ya introduce variaciones que dificultan descubrir la relación existente entre lo que vemos y el motivo del que procede el trazado.
En el resto de la nave la libertad del carpintero es total, pero tampoco es sencillo percibir el juego de ruedas existente.
Y en el presbiterio se consigue una composición totalmente distinta, separada de la anterior por un arco en el que ya vemos un intento de incorporación de las nuevas corrientes renacentistas.
En esta iglesia de un escondido pueblo abulense, el Herradón de Pinares, nos encontramos tres ricos artesonados, el de la imagen, basado en la misma rueda de nueve y doce, pero ahora utilizando cintas dobles, lo que de nuevo dificulta reconocer el motivo de origen, salvo que nos concentremos en sus faldones triangulares.
Y en un ayuntamiento cercano a Salamanca vemos de nuevo la combinación de ruedas de nueve y doce, aquí perceptible con relativa facilidad.
Esta variante en Villalcón, en la provincia de Palencia nos ofrece una nueva solución del empleo de ruedas de nueve y doce, que a pesar de realizarse en una ochava de forma similar a la anterior, nada tiene que ver con la traza vista en la anterior imagen.
Y en Tordesillas encontramos este espectacular artesonado que cubre la iglesia del convento de Santa Clara. Siempre partiendo de las ruedas de nueve y doce, pero el motivo básico apenas se percibe en el conjunto.
Tampoco es fácil comprobar que de nuevo este artesonado de la escalera del palacio de Buenavista de Málaga, donde compite con las pinturas de Picasso, depende exclusivamente de las ruedas de nueve y doce
O esta joya de la carpintería palentina, en Cisneros, antes de su restauración
Y aquí un detalle de la misma, después de ser restaurada, también basada en las ruedas de nueve y doce
Como está de la Sala del Solio del Alcázar segoviano, que tal vez nos recuerda a la salmantina vista antes, pero que sin embargo, es distinta de aquella.
O ésta de la Sala Capitular del convento de San Antonio el Real, de Segovia, también es una ochava, pero las dimensiones de los faldones ahora son completamente distintas de los antes vistos y el resultado, lógicamente poco se parece a los anteriores.
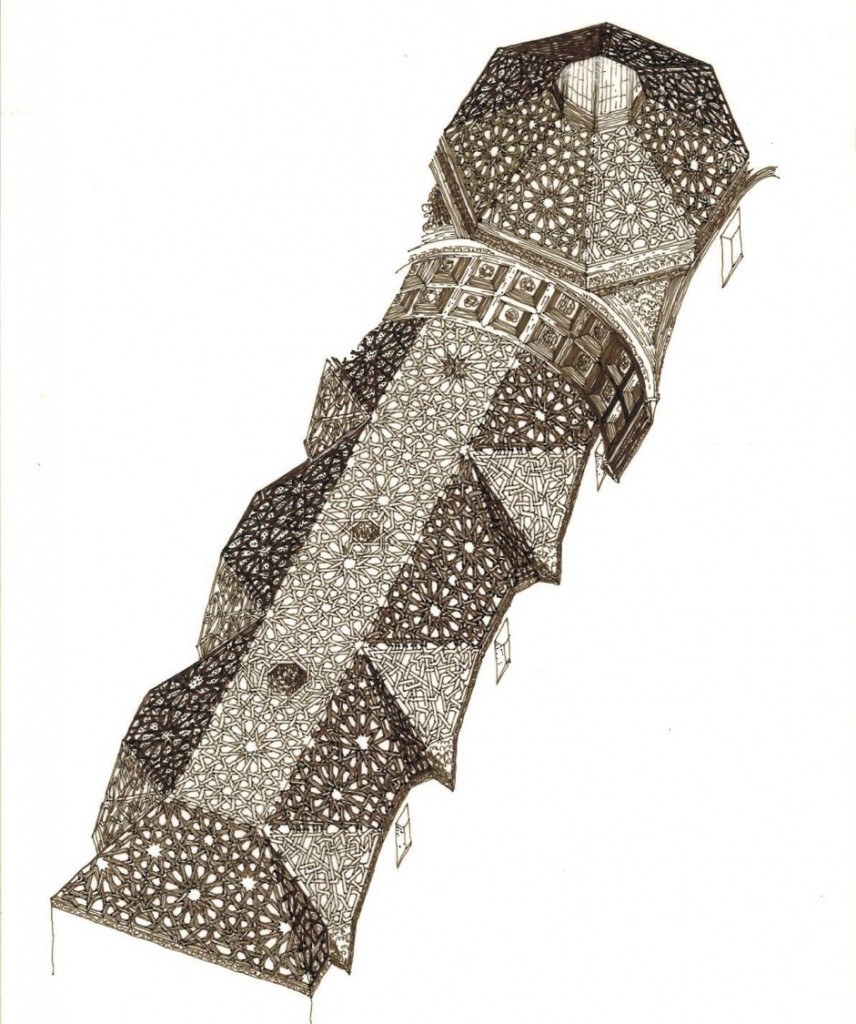
Esta sólo podemos imaginarla a través de esta perspectiva que he podido realizar a partir de los restos que se conservan en los almacenes de la Alhambra, y a una antigua fotografía en la que se podían apreciar los tejados de la iglesia de San Gil, desaparecida al construir la Gran Vía.
Y aunque a primera vista puede parecernos que se trata de una nueva combinación de ruedas de nueve y doce, basta fijarnos detenidamente para darnos cuenta que son ruedas de diez y veinte brazos, pero si no estamos acostumbrados tal vez nos cueste percibir la diferencia.
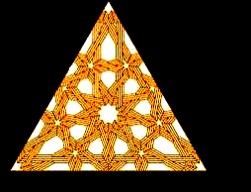
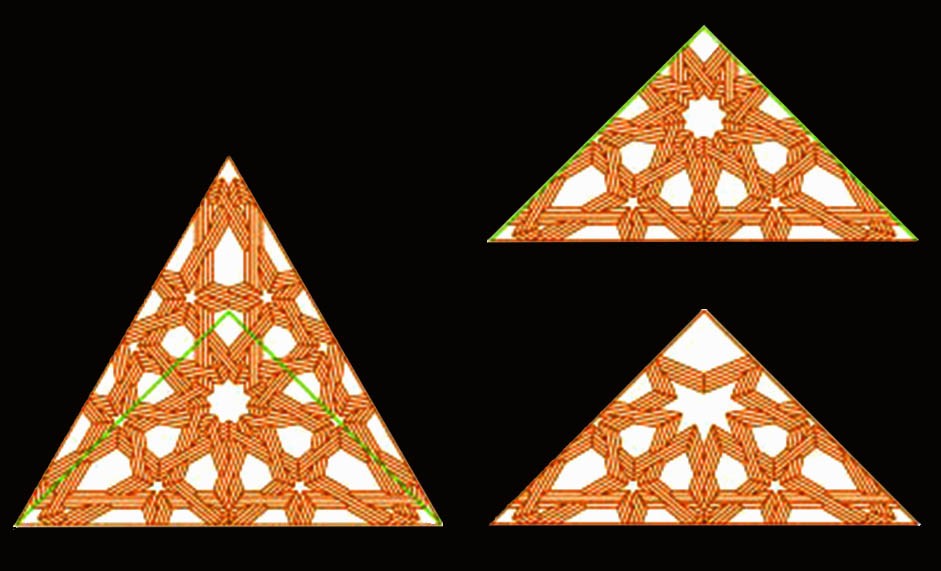
Voy a terminar con los dibujos que han dado motivo a esta charla, cuyos trazados también están basados en las ruedas de nueve y doce brazos, este ejemplo ya lo vimos antes, en la iglesia palentina de Cisneros
Y finalmente, el segundo dibujo, que es otro ejemplo de lo que puede dar de si la rueda de nueve y su desculatada de doce, pero lo más interesante de todo es la facilidad con que cualquier carpintero podría copiar la idea y reproducir de memoria todo este complejo artesonado, con sólo recordar de memoria que el almizate era un triángulo equilátero, que los faldones son triángulos y cuadrados alternados, y que el conjunto formado con el almizate y los faldones quedaba finalmente inscrito en un rectángulo, lo que requiere unas pechinas que por fuerza de la geometría son medios triángulos equiláteros.